Last update: 21.11.2021. All opinions are my own.
1. Overview
Estimating text complexity and readability is a crucial task for teachers. Offering students text passages at the right level of challenge is important for facilitating a fast development of reading skills. The existing tools to estimate readability rely on weak proxies and heuristics. Deep learning may help to improve the accuracy of the used text complexity scores.
This blog post overviews an interactive web app that estimates reading complexity of a custom text with deep learning. The app relies on transformer models that are part of my top-9% solution to the CommonLit Readability Prize Kaggle competition. The app is built in Python and deployed in Streamlit. The blog post provides a demo of the app and includes a summary of the modeling pipeline and the app implementation.
2. App demo
You can open the app by clicking on this link. Alternatively, just scroll down to see the app embedded in this blog post. If the embedded version does not load, please open the app in a new tab. Feel free to play around with the app by typing or pasting custom texts and estimating their complexity with different models! Scroll further down to read some details on the app and the underlying models.
3. Implementation
3.1. Modeling pipeline
The app is developed in the scope of the CommonLit Readability Prize Kaggle competition on text complexity prediction. My solution is an ensemble of eight transformer models, including variants of BERT, RoBERTa and other architectures. All transformers are implemented in PyTorch and feature a custom regression head that uses a concatenated output of multiple hidden layers.
The project uses pre-trained transformer weights published on the HuggingFace model hub. Each model is then fine-tuned on a data set with 2834 text snippets, where readability of each snippet was evaluated by human experts. To avoid overfitting, fine-tuning relies on text augmentations such as sentence order shuffle, backtranslation and injecting target noise in the readability scores.
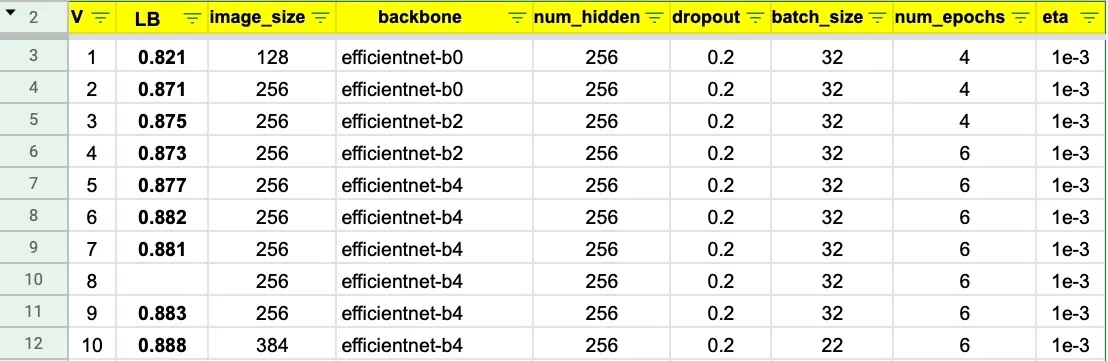
Each transformer model is fine-tuned using five-fold cross-validation repeated three times with different random splits. This GitHub repo provides the source code and documentation for the modeling pipeline. The table below summarizes the main architecture and training parameters.
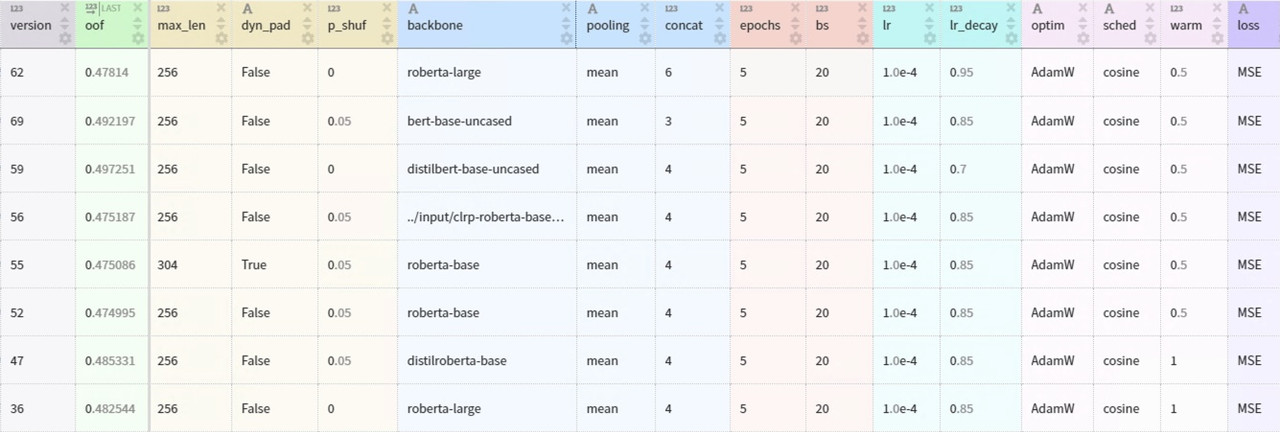
The ensemble of eight transformer models places in the top-9% of the Kaggle competition leaderboard. The web app only includes two lightweight models from a single fold to ensure fast inference on CPU: DistilBERT and DistilRoBERTa.
3.2. App implementation
The app is built in Python using the Streamlit library. Streamlit allows implementing a web app in a single Python code file and deploying the app to the cloud server so that anyone with the Internet access can check it out.
The app code is provided in web_app.py located in the root folder of the project GitHub repo. The app is hosted on a virtual machine provided by Streamlit, which includes the list of dependencies specified in requirements.txt. It also imports some helper functions used within the modeling pipeline for text preprocessing and model initialization.
The app works by downloading weights of the selected transformer model to the virtual machine after a user selects which model to use for text readability prediction. The weights of each model are made available as release files on GitHub. After downloading the weights, the app transforms the text entered by a user into the token sequence with the tokenizer that uses text processing settings specified in the model configuration file. Next, the app runs a single forward pass through the initialized transformer network and displays the output prediction.
The snippet below provides the app source code. The code imports relevant Python modules and configures the app page. Next, it provides functionality for entering the custom text and selecting the NLP model. Finally, the code includes the inference function and some further documentation.
#collapse-show
##### PREPARATIONS
# libraries
import gc
import os
import pickle
import sys
import urllib.request
import requests
import numpy as np
import pandas as pd
import streamlit as st
from PIL import Image
# custom libraries
sys.path.append('code')
from model import get_model
from tokenizer import get_tokenizer
# download with progress bar
mybar = None
def show_progress(block_num, block_size, total_size):
global mybar
if mybar is None:
mybar = st.progress(0.0)
downloaded = block_num * block_size / total_size
if downloaded <= 1.0:
mybar.progress(downloaded)
else:
mybar.progress(1.0)
# page config
st.set_page_config(page_title = "Readability prediction",
page_icon = ":books:",
layout = "centered",
initial_sidebar_state = "collapsed",
menu_items = None)
##### HEADER
# title
st.title('Text readability prediction')
# image cover
image = Image.open(requests.get('https://i.postimg.cc/hv6yfMYz/cover-books.jpg', stream = True).raw)
st.image(image)
# description
st.write('This app uses deep learning to estimate the reading complexity of a custom text. Enter your text below, and we will run it through one of the two transfomer models and display the result.')
##### PARAMETERS
# title
st.header('How readable is your text?')
# model selection
model_name = st.selectbox(
'Which model would you like to use?',
['DistilBERT', 'DistilRoBERTa'])
# input text
input_text = st.text_area('Which text would you like to rate?', 'Please enter the text in this field.')
##### MODELING
# compute readability
if st.button('Compute readability'):
# specify paths
if model_name == 'DistilBERT':
folder_path = 'output/v59/'
weight_path = 'https://github.com/kozodoi/Kaggle_Readability/releases/download/0e96d53/weights_v59.pth'
elif model_name == 'DistilRoBERTa':
folder_path = 'output/v47/'
weight_path = 'https://github.com/kozodoi/Kaggle_Readability/releases/download/0e96d53/weights_v47.pth'
# download model weights
if not os.path.isfile(folder_path + 'pytorch_model.bin'):
with st.spinner('Downloading model weights. This is done once and can take a minute...'):
urllib.request.urlretrieve(weight_path, folder_path + 'pytorch_model.bin', show_progress)
# compute predictions
with st.spinner('Computing prediction...'):
# clear memory
gc.collect()
# load config
config = pickle.load(open(folder_path + 'configuration.pkl', 'rb'))
config['backbone'] = folder_path
# initialize model
model = get_model(config, name = model_name.lower(), pretrained = folder_path + 'pytorch_model.bin')
model.eval()
# load tokenizer
tokenizer = get_tokenizer(config)
# tokenize text
text = tokenizer(text = input_text,
truncation = True,
add_special_tokens = True,
max_length = config['max_len'],
padding = False,
return_token_type_ids = True,
return_attention_mask = True,
return_tensors = 'pt')
inputs, masks, token_type_ids = text['input_ids'], text['attention_mask'], text['token_type_ids']
# clear memory
del tokenizer, text, config
gc.collect()
# compute prediction
if input_text != '':
prediction = model(inputs, masks, token_type_ids)
prediction = prediction['logits'].detach().numpy()[0][0]
prediction = 100 * (prediction + 4) / 6 # scale to [0,100]
# clear memory
del model, inputs, masks, token_type_ids
gc.collect()
# print output
st.metric('Readability score:', '{:.2f}%'.format(prediction, 2))
st.write('**Note:** readability scores are scaled to [0, 100%]. A higher score means that the text is easier to read.')
st.success('Success! Thanks for scoring your text :)')
##### DOCUMENTATION
# header
st.header('More information')
# example texts
with st.expander('Show example texts'):
st.table(pd.DataFrame({
'Text': ['A dog sits on the floor. A cat sleeps on the sofa.', 'This app does text readability prediction. How cool is that?', 'Training of deep bidirectional transformers for language understanding.'],
'Score': [1.5571, -0.0100, -2.4025],
}))
# models
with st.expander('Read about the models'):
st.write("Both transformer models are part of my top-9% solution to the CommonLit Readability Kaggle competition. The pre-trained language models are fine-tuned on 2834 text snippets. [Click here](https://github.com/kozodoi/Kaggle_Readability) to see the source code and read more about the training pipeline.")
# metric
with st.expander('Read about the metric'):
st.write("The readability metric is calculated on the basis of a Bradley-Terry analysis of more than 111,000 pairwise comparisons between excerpts. Teachers spanning grades 3-12 (a majority teaching between grades 6-10) served as the raters for these comparisons. More details on the used reading complexity metric are available [here](https://www.kaggle.com/c/commonlitreadabilityprize/discussion/240886).")
4. Closing words
This blog post provided a demo of an interactive web app that uses deep learning to estimate text reading complexity. I hope you found the app interesting and enjoyed playing with it!
If you have any data science projects in your portfolio, I highly encourage you to try developing a similar app yourself. There are many things you could demonstrate, ranging from interactive EDA dashboards to inference calls to custom ML models. Streamlit makes this process very simple and allows hosting the app in the cloud. Happy learning!