Test-Time Augmentation for Tabular Data
Improving predictive performance during inference

- 1. Overview
- 2. Adapting TTA to tabular data
- 3. Implementing TTA
- 4. Empirical benchmark
- 5. Closing words
1. Overview
Test time augmentation (TTA) is a popular technique in computer vision. TTA aims at boosting the model accuracy by using data augmentation on the inference stage. The idea behind TTA is simple: for each test image, we create multiple versions that are a little different from the original (e.g., cropped or flipped). Next, we predict labels for the test images and created copies and average model predictions over multiple versions of each image. This usually helps to improve the accuracy irrespective of the underlying model.
In many business settings, data comes in a tabular format. Can we use TTA with tabular data to enhance the accuracy of ML models in a way similar to computer vision models? How to define suitable transformations of test cases that do not affect the label? This blog post explores the opportunities for using TTA in tabular data environments. We will implement TTA for scikit-learn classifiers and test its performance on multiple credit scoring data sets. The preliminary results indicate that TTA might be a tiny bit helpful in some settings.
Note: the results presented in this blog post are currently being extended within a scope of a working paper. The post will be updated once the paper is available on ArXiV.
2. Adapting TTA to tabular data
TTA has been originally developed for deep learning applications in computer vision. In contrast to image data, tabular data poses a more challenging environment for using TTA. We will discuss two main challenges that we need to solve to apply TTA to structured data:
- how to define transformations?
- how to treat categorical features?
2.1. How to define transformations?
When working with image data, light transformations such as rotation, brightness adjustment, saturation and many others modify the underlying pixel values but do not affect the ground truth. That is, a rotated cat is still a cat. We can easily verify this by visually checking the transformed images and limiting the magnitude of transformations to make sure the cat is still recognizable.

This is different for tabular data, where the underlying features represent different characteristics of the observed subjects. Let's consider a credit scoring example. In finance, banks use ML models to support loan allocation decisions. Consider a binary classification problem, where we predict whether the applicant will pay back the loan. The underlying features may describe the applicant's attributes (age, gender), loan parameters (amount, duration), macroeconomic indicators (inflation, growth). How to do transformations on these features? While there is no such thing as rotating a loan applicant (at least not within the scope of machine learning), we could do a somewhat similar exercise: create copies of each loan applicant and slightly modify feature values for each copy. A good starting point would be to add some random noise to each of the features.
This procedure raises a question: how can we be sure that transformations do not alter the label? Would increasing the applicant's age by 10 years affect her repayment ability? Arguably, yes. What about increasing the age by 1 year? Or 1 day? These are challenging questions that we can not answer without more information. This implies that the magnitude of the added noise has to be carefully tuned. We need to take into account the variance of each specific feature as well as the overall data set variability. Adding too little noise will create synthetic cases that are too similar to the original applications, which is not very useful. On the other hand, adding too much noise risks changing the label of the corresponding application, which would harm the model accuracy. The trade-off between these two extremes is what can potentially bring us closer to discovering an accuracy boost.
2.2. How to treat categorical features?
It is rather straightforward to add noise to continuous features such as age or income. However, tabular data frequently contains special gifts: categorical features. From gender to zip code, these features present another challenge for the application of TTA. Adding noise to the zip code appears non-trivial and requires some further thinking. Ignoring categorical features and only altering the continuous ones sounds like an easy solution, but this might not work well on data sets that contain a lot of information in the form of categorical data.
In this blog post, we will try a rather naive approach to deal with categorical features. Every categorical feature can be encoded as a set of dummy variables. Next, considering each dummy feature separately, we can occasionally flip the value, switching the person's gender, country of origin or education level with one click. This would introduce some variance in the categorical features and provide TTA with more diverse synthetic applications. This approach is imperfect and can be improved on, but we have to start somewhere, right?
Now that we have some ideas about how TTA should work and what are the main challenges, let's actually try to implement it!
3. Implementing TTA
This section implements a helper function predict_proba_with_tta() to extend the standard predict_proba() method in scikit-learn such that predictions take advantage of the TTA procedure. We focus on a binary classification task, but one could easily extend this framework to regression tasks as well.
The function predict_proba_with_tta() requires specifying the underlying scikit-learn model and the test set with observations to be predicted. The function operates in four simple steps:
- Creating
num_ttacopies of the test set. - Implementing random transformations of the synthetic copies.
- Predicting labels for the real and synthetic observations.
- Aggregating the predictions.
Considering the challenges discussed in the previous section, we implement the following transformations for the continuous features:
- compute STD of each continuous feature denoted as
std - generate a random vector
nusing the standard normal distribution - add
alpha * n * stdto each feature , wherealphais a meta-parameter.
And for the categorical features:
- convert categorical features into a set of dummies
- flip each dummy variable with a probability
beta, wherebetais a meta-parameter.
By varying alpha and beta, we control the transformation magnitude, adjusting the noise scale in the synthetic copies. Higher values imply stronger transformations. The suitable values can be identified through some meta-parameter tuning.
#collapse-show
def predict_proba_with_tta(data,
model,
dummies = None,
num_tta = 4,
alpha = 0.01,
beta = 0.01,
seed = 0):
'''
Predicts class probabilities using TTA.
Arguments:
- data (numpy array): data set with the feature values
- model (sklearn model): machine learning model
- dummies (list): list of column names of dummy features
- num_tta (integer): number of test-time augmentations
- alpha (float): noise parameter for continuous features
- beta (float): noise parameter for dummy features
- seed (integer): random seed
Returns:
- array of predicted probabilities
'''
# set random seed
np.random.seed(seed = seed)
# original prediction
preds = model.predict_proba(data) / (num_tta + 1)
# select numeric features
num_vars = [var for var in data.columns if data[var].dtype != 'object']
# find dummies
if dummies != None:
num_vars = list(set(num_vars) - set(dummies))
# synthetic predictions
for i in range(num_tta):
# copy data
data_new = data.copy()
# introduce noise to numeric vars
for var in num_vars:
data_new[var] = data_new[var] + alpha * np.random.normal(0, 1, size = len(data_new)) * data_new[var].std()
# introduce noise to dummies
if dummies != None:
for var in dummies:
probs = np.random.binomial(1, (1 - beta), size = len(data_new))
data_new.loc[probs == 0, var] = 1 - data_new.loc[probs == 0, var]
# predict probs
preds_new = model.predict_proba(data_new)
preds += preds_new / (num_tta + 1)
# return probs
return preds
4. Empirical benchmark
Let's test our TTA function! This section performs empirical experiment on multiple data sets to check whether TTA can improve the model performance. First, we import relevant modules and load the list of prepared data sets. All data sets come from a credit scoring environment, which represents a binary classification setup. Some of the data sets are publically available, whereas the others are subject to NDA. The public data sets include australian), german), pakdd, gmsc, homecredit and lendingclub. The sample sizes and the number of features vary greatly across the datasets. This allows us to test the TTA framework in different conditions.
#collapse-hide
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import roc_auc_score
import os
import time
#collapse-show
datasets = os.listdir('../data')
datasets
Apart from the data sets, TTA needs an underlying ML model. In our experiment, on each data set, we will use a Random Forest classifier with 500 trees, which is a good trade-off between good performance and computational resources. We will not go deep into tuning the classifier and keep the parameters fixed for all data sets. We will then use stratified 5-fold cross-validation to train and test models with and without TTA.
#collapse-show
# classifier
clf = RandomForestClassifier(n_estimators = 500, random_state = 1, n_jobs = 4)
# settings
folds = StratifiedKFold(n_splits = 5,
shuffle = True,
random_state = 23)
The cell below implements the following experiment:
- We loop through the datasets and perform cross-validation, training Random Forest on each fold combination.
- Next, we predict labels of the validation cases and calculate the AUC of the model predictions. This is our benchmark.
- We predict labels of the validation cases with the same model but now implement TTA to adjust the predictions.
- By comparing the average AUC difference before and after TTA, we can judge whether TTA actually helps to boost the predictive performance.
#collapse-show
# placeholders
auc_change = []
# timer
start = time.time()
# modeling loop
for data in datasets:
##### DATA PREPARATION
# import data
X = pd.read_csv('../data/' + data)
# convert target to integer
X.loc[X.BAD == 'BAD', 'BAD'] = 1
X.loc[X.BAD == 'GOOD', 'BAD'] = 0
# extract X and y
y = X['BAD']
del X['BAD']
# create dummies
X = pd.get_dummies(X, prefix_sep = '_dummy_')
# data information
print('-------------------------------------')
print('Dataset:', data, X.shape)
print('-------------------------------------')
##### CROSS-VALIDATION
# create objects
oof_preds_raw = np.zeros((len(X), y.nunique()))
oof_preds_tta = np.zeros((len(X), y.nunique()))
# modeling loop
for fold_, (trn_, val_) in enumerate(folds.split(y, y)):
# data partitioning
trn_x, trn_y = X.iloc[trn_], y.iloc[trn_]
val_x, val_y = X.iloc[val_], y.iloc[val_]
# train the model
clf.fit(trn_x, trn_y)
# identify dummies
dummies = list(X.filter(like = '_dummy_').columns)
# predictions
oof_preds_raw[val_, :] = clf.predict_proba(val_x)
oof_preds_tta[val_, :] = predict_proba_with_tta(data = val_x,
model = clf,
dummies = dummies,
num_tta = 5,
alpha = np.sqrt(len(trn_x)) / 3000,
beta = np.sqrt(len(trn_x)) / 30000,
seed = 1)
# print performance
print('- AUC before TTA = %.6f ' % roc_auc_score(y, oof_preds_raw[:,1]))
print('- AUC with TTA = %.6f ' % roc_auc_score(y, oof_preds_tta[:,1]))
print('-------------------------------------')
print('')
# save the AUC delta
delta = roc_auc_score(y, oof_preds_tta[:,1]) - roc_auc_score(y, oof_preds_raw[:,1])
auc_change.append(delta)
# display results
print('-------------------------------------')
print('Finished in %.1f minutes' % ((time.time() - start) / 60))
print('-------------------------------------')
print('TTA improves AUC in %.0f/%.0f cases' % (np.sum(np.array(auc_change) > 0), len(datasets)))
print('Mean AUC change = %.6f' % np.mean(auc_change))
print('-------------------------------------')
Looks like TTA is working! Overall, TTA improves the AUC in 10 out of 12 data sets. The observed performance gains are rather small: on average, TTA improves AUC by 0.00236. The results are visualized in the barplot below:
#collapse-hide
objects = list(range(len(datasets)))
y_pos = np.arange(len(objects))
perf = np.sort(auc_change2)
plt.figure(figsize = (6, 8))
plt.barh(y_pos, perf, align = 'center', color = 'blue', alpha = 0.66)
plt.ylabel('Dataset')
plt.yticks(y_pos, objects)
plt.xlabel('AUC Gain')
plt.title('')
ax.plot([0, 0], [1, 12], 'k--')
plt.tight_layout()
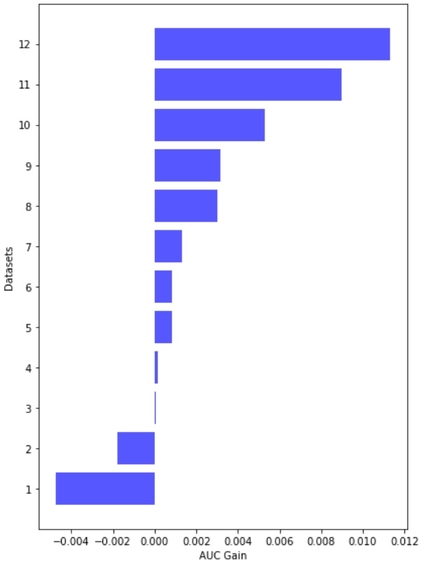
We should bear in mind that performance gains, although appearing rather small, come almost "for free". We don't need to train a new model and only require a relatively small amount of extra resources to create synthetic copies of the loan applications. Sounds good!
It is possible that further fine-tuning of the TTA meta-parameters can uncover larger performance gains. Furthermore, a considerable variance of the average gains from TTA across the data sets indicates that TTA can be more helpful in specific settings. The important factors influencing the TTA performance may relate to both the data and the classifier used to produce predictions. More research is needed to identify and analyze such factors.
5. Closing words
The purpose of this tutorial was to explore TTA applications for tabular data. We have discussed the corresponding challenges, developed a TTA wrapper function for scikit-learn and demonstrated that it could indeed be helpful on multiple credit scoring data sets. I hope you found this post interesting.
The project described in this blog post is a work in progress. I will update the post once the working paper on the usage of TTA for tabular data is available. Stay tuned and happy learning!
Liked the post? Share it on social media!
You can also buy me a cup of tea to support my work. Thanks!
